Home › Cubo 2x2x2 › Método de Guimond

Método de Guimond

O método de Guimond foi desenvolvido por Gaétan Guimond, na década de 80, e é um método que permite resolver um 2×2 orientando primeiro todos os cantos e depois permutando ambas as camadas. Requer 16 algoritmos (sem casos equivalentes).

Passo 1: Resolver 3/4 de uma face com cores opostas

Deve-se entender aqui cores opostas como cores que aparecem em lados opostos do cubo. No caso do esquema de cores tradicional, são verde/azul, branco/amarelo e vermelho/laranja. Na grande maioria dos casos, se não existir nenhuma face nestas condições,

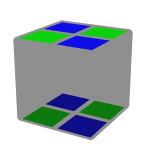
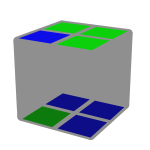
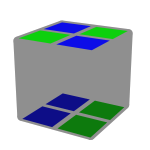
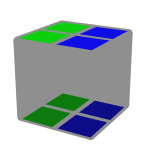
Eis alguns exemplos de 3/4 de uma face resolvida utilizando cores opostas.

2x2 Guimond Face Exemplo 1
Exemplo 1
2x2 Guimond Face Exemplo 2
Exemplo 2
2x2 Guimond Face Exemplo 3
Exemplo 3
2x2 Guimond Face Exemplo 4
Exemplo 4
2x2 Guimond Face Exemplo 5
Exemplo 5

Como se pode verificar no exemplo 5, não é necessário que essa face parcial tenha que ser constituída sempre por cores opostas. Pode-se usar uma mesma cor ou cores opostas.

Pode-se igualmente observar que os exemplos 1 e 2 são em tudo semelhantes, exceto na orientação do 4º canto que não está bem orientado. Deve-se tomar isso em conta para a correta identificação do caso a executar no passo seguinte.

Passo 2: Orientação dos cantos

Coloca-se a face construída no passo anterior para baixo e, consoante a orientação do último canto não orientado (horária ou anti-horária), executam-se os algoritmos de acordo com as hipóteses apresentadas.

Note-se que se vai usar a cor rosa/roxo para simbolizar cores opostas, isto é, os autocolantes representados nas imagens seguintes podem simbolizar qualquer cor oposta, como no primeiro passo.

Orientação “anti-horária”

2x2 Guimond Orientação 1
F’ L2 F
2x2 Guimond Orientação 2
L2 U L
2x2 Guimond Orientação 3
R2 F2 U F
2x2 Guimond Orientação 4
L U’ L’

2x2 Guimond Orientação 5
y’ R’ F’ R
2x2 Guimond Orientação 6
x2 R U’ B L’
2x2 Guimond Orientação 7
F’ R U’ F2 U’
2x2 Guimond Orientação 8
R F2 U’ R2 F U’

Orientação “horária”

2x2 Guimond Orientação 9
L U2 L’
2x2 Guimond Orientação 10
y L2 D’ R
2x2 Guimond Orientação 11
F2 R2 U’ R’
2x2 Guimond Orientação 12
y R’ U R

2x2 Guimond Orientação 13
L U L’
2x2 Guimond Orientação 14
R U’ B L’
2x2 Guimond Orientação 15
R’ F U’ F2 U
2x2 Guimond Orientação 16
x U R’ U’ R U2 R

Passo 3: Resolver faces opostas

Após a orientação dos cantos, resolvem-se as faces opostas.

Há 4 hipóteses relevantes:

2x2 Guimond Permutação 1
R2 U2 F2
2x2 Guimond Permutação 2
R2 U’ R2′
2x2 Guimond Permutação 3
R2 U’ R2′ U’ R2
2x2 Guimond Permutação 4
R2

Passo 4: Permutar ambas as camadas

Este passo é exatamente igual ao passo de permutação de ambas as camadas do método Ortega.